There are a couple of facts about superellipsoids we should know. First, we should not use a value of 0 for either r nor n. This will cause POV-Ray to incorrectly make a black box instead of our desired shape. Second, very small values of r and n may yield strange results so they should be avoided. Finally, the Sturmian root solver will not work with superellipsoids.
Superellipsoids are finite objects so they respond to auto-bounding and can be used in CSG.
Now let's use the superellipsoid to make something that would be useful in a scene. We will make a tiled floor and place a couple of superellipsoid objects hovering over it. We can start with the file we have already made.
We rename it to tiles.pov and edit it so that it reads as follows:
Note that we have added #include "textures.inc" so we can use pre-defined textures. Now we want to define the superellipsoid which will be our tile.
Superellipsoids are roughly 2*2*2 units unless we scale them otherwise. If we wish to lay a bunch of our tiles side by side, they will have to be offset from each other so they don't overlap. We should select an offset value that is slightly more than 2 so that we have some space between the tiles to fill with grout. So we now add this:
We now want to lay down a row of tiles. Each tile will be offset from the original by an ever-increasing amount in both the +z and -z directions. We refer to our offset and multiply by the tile's rank to determine the position of each tile in the row. We also union these tiles into a single object called Row like this:
This gives us a single row of 17 tiles, more than enough to fill the screen. Now we must make copies of the Row and translate them, again by the offset value, in both the +x and -x directions in ever increasing amounts in the same manner.
Finally, our tiles are complete. But we need a texture for them. To do this we union all of the Rows together and apply a White Marble pigment and a somewhat shiny reflective surface to it:
We now need to add the grout. This can simply be a white plane. We have stepped up the ambient here a little so it looks whiter.
To complete our scene, let's add five different superellipsoids, each a different color, so that they hover over our tiles and are reflected in them.

Some superellipsoids hovering above a tiled floor.
We trace the scene at 320x200 -A to see the result. If we are happy with that, we do a final trace at 640x480 +A0.2.
We first start by thinking about the shape of the final object. It is quite difficult to come up with a set of points that describe a given curve without the help of a modelling program supporting POV-Eay's surface of revolution object. If such a program is available we should take advantage of it.
We will use the point configuration shown in the figure above. There are eight points describing the curve that will be rotated about the y-axis to get our cup. The curve was calculated using the method described in the reference section (see "Surface of Revolution").
Now it is time to come up with a scene that uses the above SOR object. We edit a file called sordemo.pov and enter the following text.
The scene contains our cup object resting on a checkered plane. Tracing this scene at a resolution of 320x200 results in the image below.
The surface of revolution is described by starting with the number of points followed by the points with ascending heights. Each point determines the radius the curve for a given height. E. g. the first point tells POV-Ray that at height -0.5 the radius is 0. We should take care that each point has a larger height than its predecessor. If this is not the case the program will abort with an error message.
Section 4.4.9
Surface of Revolution Object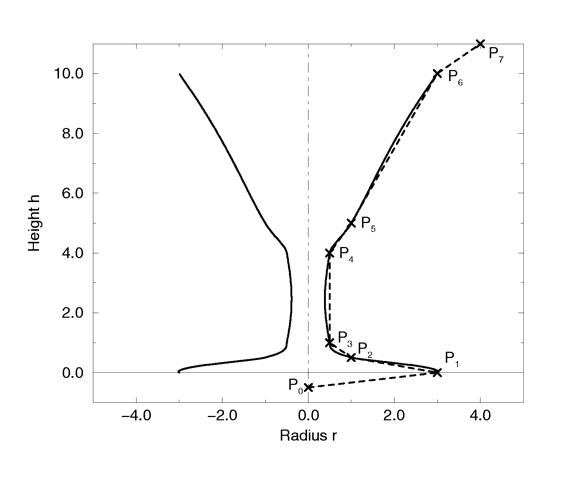
The point configuration of our cup object.

A surface of revolution object.
Table Of Contents