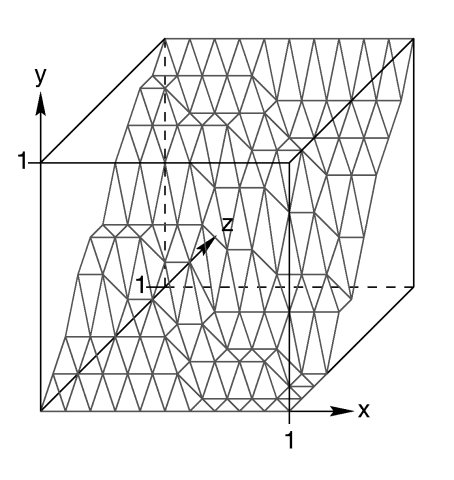
The size and orientation of an un-scaled height field.
A height field is essentially a one unit wide by one unit long square with a mountainous surface on top. The height of the mountain at each point is taken from the color number or palette index of the pixels in a graphic image file. The maximum height is one, which corresponds to the maximum possible color or palette index value in the image file.

The mesh of triangles corresponds directly to the pixels in the image file. Each square formed by four neighboring pixels is divided into two triangles. An image with a resolution of N*M pixels has (N-1)*(M-1) squares that are divided into 2*(N-1)*(M-1) triangles.
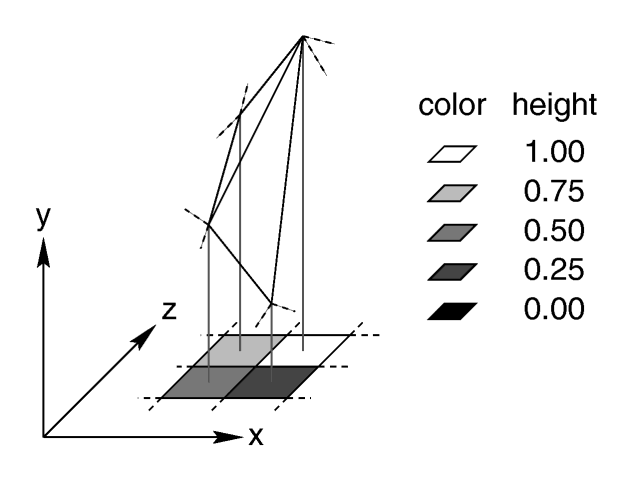
The resolution of the height field is influenced by two factors: the resolution of the image and the resolution of the color/index values. The size of the image determines the resolution in the x- and z-direction. A larger image uses more triangles and looks smoother. The resolution of the color/index value determines the resolution along the y-axis. A height field made from an 8 bit image can have 256 different height levels while one made from a 16 bit image can have up to 65536 different height levels. Thus the second height field will look much smoother in the y-direction if the height field is created appropriately.
The size/resolution of the image does not affect the size of the height field. The un-scaled height field size will always be 1* 1. Higher resolution image files will create smaller triangles, not larger height fields.
There are six or possibly seven types of files which can define a heightfield, as follows:
The image file used to create a height field can be a GIF, TGA, POT, PNG, PGM, PPM and possibly a system specific (e. g. Windows BMP or Macintosh Pict) format file. The GIF, PNG, PGM and possibly system format files are the only ones that can be created using a standard paint program. Though there are paint programs for creating TGA image files they won't be of much use for creating the special 16 bit TGA files used by POV-Ray (see below and "HF_Gray_16" for more details).
In an image file like GIF that uses a color palette the color number is the palette index at a given pixel. Use a paint program to look at the palette of a GIF image. The first color is palette index zero, the second is index one, the third is index two and so on. The last palette entry is index 255. Portions of the image that use low palette entries will result in lower parts of the height field. Portions of the image that use higher palette entries will result in higher parts of the height field.
Height fields created from GIF files can only have 256 different height levels because the maximum number of colors in a GIF file is 256.
The color of the palette entry does not affect the height of the pixel. Color entry 0 could be red, blue, black or orange but the height of any pixel that uses color entry 0 will always be 0. Color entry 255 could be indigo, hot pink, white or sky blue but the height of any pixel that uses color entry 255 will always be 1.
You can create height field GIF images with a paint program or a fractal program like Fractint. You can usually get Fractint from most of the same sources as POV-Ray.
A POT file is essentially a GIF file with a 16 bit palette. The maximum number of colors in a POT file is 65536. This means a POT height field can have up to 65536 possible height values. This makes it possible to have much smoother height fields. Note that the maximum height of the field is still 1 even though more intermediate values are possible.
At the time of this writing the only program that created POT files was a freeware IBM-PC program called Fractint. POT files generated with this fractal program create fantastic landscapes.
The TGA and PPM file formats may be used as a storage device for 16 bit numbers rather than an image file. These formats use the red and green bytes of each pixel to store the high and low bytes of a height value. These files are as smooth as POT files but they must be generated with special custom-made programs. Several programs can create TGA heightfields in the format POV uses, such as gforge and Terrain Maker.
PNG format heightfields are usually stored in the form of a grayscale image with black corresponding to lower and white to higher parts of the height field. Because PNG files can store up to 16 bits in grayscale images they will be as smooth as TGA and PPM images. Since they are grayscale images you will be able to view them with a regular image viewer. gforge can create 16-bit heightfields in PNG format. Color PNG images will be used in the same way as TGA and PPM images.
SYS format is a platform specific file format. See your platform specific documentation for details.
An optional water_level parameter may be added after the file name. It consists of the keyword water_level followed by a float value telling the program to ignore parts of the height field below that value. The default value is zero and legal values are between zero and one. For example water_level .5 tells POV-Ray to only render the top half of the height field. The other half is below the water and couldn't be seen anyway. This term comes from the popular use of height fields to render landscapes. A height field would be used to create islands and another shape would be used to simulate water around the islands. A large portion of the height field would be obscured by the water so the water_level parameter was introduced to allow the ray-tracer to ignore the unseen parts of the height field. water_level is also used to cut away unwanted lower values in a height field. For example if you have an image of a fractal on a solid colored background, where the background color is palette entry 0, you can remove the background in the height field by specifying, water_level .001.
Normally height fields have a rough, jagged look because they are made of lots of flat triangles. Adding the keyword smooth causes POV-Ray to modify the surface normal vectors of the triangles in such a way that the lighting and shading of the triangles will give a smooth look. This may allow you to use a lower resolution file for your height field than would otherwise be needed. However, smooth triangles will take longer to render.
In order to speed up the intersection tests an one-level bounding hierarchy is available. By default it is always used but it can be switched off to eventually improve the rendering speed for small height fields (i. e. low resolution images).
The julia_fractal syntax (with default values listed in comments) is:
The 4-D vector 4DJULIA_PARAMETER is the classic Julia parameter p in the iterated formula f(h) + p.
The julia fractal object is calculated by using an algorithm that determines whether an arbitrary point h(0) in 4-D space is inside or outside the object. The algorithm requires generating the sequence of vectors h(0), h(1), ... by iterating the formula
where p is the fixed 4-D vector parameter of the julia fractal and f() is one of the functions sqr, cube, ... specified by the presence of the corresponding keyword. The point h(0) that begins the sequence is considered inside the julia fractal object if none of the vectors in the sequence escapes a hypersphere of radius 4 about the origin before the iteration number reaches the max_iteration value. As you increase max_iteration, some points escape that did not previously escape, forming the julia fractal. Depending on the JULIA_PARAMETER, the julia fractal object is not necessarily connected; it may be scattered fractal dust. Using a low max_iteration can fuse together the dust to make a solid object. A high max_iteration is more accurate but slows rendering. Even though it is not accurate, the solid shapes you get with a low_maximum iteration value can be quite interesting.
Since the mathematical object described by this algorithm is four-dimensional and POV-Ray renders three dimensional objects, there must be a way to reduce the number of dimensions of the object from four dimensions to three. This is accomplished by intersecting the 4-D fractal with a 3-D plane defined by the slice field and then projecting the intersection to 3-D space. The slice plane is the 3-D space that is perpendicular to NORMAL4D and is DISTANCE units from the origin. Zero length NORMAL4D vectors or a NORMAL4D vector with a zero fourth component are illegal.
You can get a good feel for the four dimensional nature of a julia fractal by using POV-Ray's animation feature to vary a slice's DISTANCE parameter. You can make the julia fractal appear from nothing, grow, then shrink to nothing as DISTANCE changes, much as the cross section of a 3-D object changes as it passes through a plane.
The precision parameter is a tolerance used in the determination of whether points are inside or outside the fractal object. Larger values give more accurate results but slower rendering. Use as low a value as you can without visibly degrading the fractal object's appearance.
The presence of the keywords quaternion or hypercomplex determine which 4-D algebra is used to calculate the fractal. Both are 4-D generalizations of the complex numbers but neither satisfies all the field properties (all the properties of real and complex numbers that many of us slept through in high school). Quaternions have non-commutative multiplication and hypercomplex numbers can fail to have a multiplicative inverse for some non-zero elements (it has been proved that you cannot successfully generalize complex numbers to four dimensions with all the field properties intact, so something has to break). Both of these algebras were discovered in the 19th century. Of the two, the quaternions are much better known, but one can argue that hypercomplex numbers are more useful for our purposes, since complex valued functions such as sin, cos, etc. can be generalized to work for hypercomplex numbers in a uniform way.
For the mathematically curious, the algebraic properties of these two algebras can be derived from the multiplication properties of the unit basis vectors 1 = <1,0,0,0>, i=< 0,1,0,0>, j=<0,0,1,0> and k=< 0,0,0,1>. In both algebras 1 x = x 1 = x for any x (1 is the multiplicative identity). The basis vectors 1 and i behave exactly like the familiar complex numbers 1 and i in both algebras.
Quaternion basis vector multiplication rules:
Hypercomplex basis vector multiplication rules:
A distance estimation calculation is used with the quaternion calculations to speed them up. The proof that this distance estimation formula works does not generalize from two to four dimensions but the formula seems to work well anyway, the absence of proof notwithstanding!
The presence of one of the function keywords sqr, cube, etc. determines which function is used for f(h) in the iteration formula h(n+1) = f(h(n)) + p. Most of the function keywords work only if the hypercomplex keyword is present. Only sqr and cube work with quaternions. The functions are all familiar complex functions generalized to four dimensions.
A simple example of a julia fractal object is:
The first renderings of julia fractals using quaternions were done by Alan Norton and later by John Hart in the '80's. This new POV-Ray implementation follows Fractint in pushing beyond what is known in the literature by using hypercomplex numbers and by generalizing the iterating formula to use a variety of transcendental functions instead of just the classic Mandelbrot z^2 + c formula. With an extra two dimensions and eighteen functions to work with, intrepid explorers should be able to locate some new fractal beasties in hyperspace, so have at it!
Section 7.5.2.6
Julia Fractal
h(n+1) = f(h(n)) + p (n = 0, 1, ..., max_iteration-1)
ij = k; jk = i; ki = j
ji = -k; kj = -i; ik = -j
ii = jj = kk = -1; ijk = -1;
ij = k; jk = -i; ki = -j
ji = k; kj = -i; ik = -j
ii = jj = kk = -1; ijk = 1;
Function Keyword Maps 4-D value h to:
================================================
sqr h*h
cube h*h*h
exp e raised to the power h
reciprocal 1/h
sin sine of h
asin arcsine of h
sinh hyperbolic sine of h
asinh inverse hyperbolic sine of h
cos cosine of h
acos arccosine of h
cosh hyperbolic cos of h
acosh inverse hyperbolic cosine of h
tan tangent of h
atan arctangent of h
tanh hyperbolic tangent of h
atanh inverse hyperbolic tangent of h
log natural logarithm of h
pwr(x,y) h raised to the complex power x+iy
Table Of Contents