[ edito | sommaire | contribution | contacts ]
Jean Debord
JDebord@compuserve.com |
| >I. Introduction |
La transformée de Fourier est une technique mathématique permettant de déterminer le spectre de fréquences d'un signal (par exemple un son). La définition mathématique est la suivante :
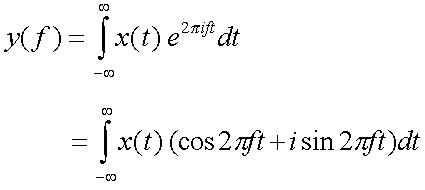
où x(t) est le signal d'entrée (fonction du temps), f la fréquence, et i la base des nombres complexes. y est la transformée de Fourier de x.
Le signal d'entrée peut être à valeurs réelles ou complexes. En revanche, la transformée de Fourier est toujours un nombre complexe. Pour chaque fréquence f, le module de y(f) représente l'énergie associée à cette fréquence. Le tracé de ce module en fonction de f constitue le spectre de fréquences du signal.
Si le signal d'entrée est échantillonné sous forme d'une suite de n valeurs x0, x1, ..., xn-1, prises à intervalles de temps constants, la transformée de Fourier se présentera sous la forme d'une suite de nombres complexes y0, y1, ..., yn-1, tels que :
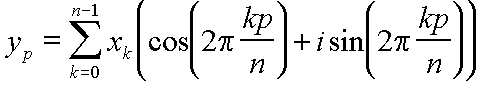 (2)
(2)
Cette formule permet, en théorie, de calculer la transformée yp en tout point. En pratique, on utilise habituellement un algorithme plus rapide, appelé transformée de Fourier rapide (Fast Fourier Transform, FFT).
Pour plus de précisions sur la FFT et ses applications, nous renvoyons à la page de Don Cross, dont une traduction française est disponible sur ce site.
Pour une présentation plus mathématique de l'algorithme FFT, nous renvoyons au site de J. Beuneu.
| >II. Programmation en Turbo Pascal |
Le calcul de la transformée de Fourier peut être réalisé au moyen de la bibliothèque TP MATH. Les programmes de cette librairie sont adaptés de ceux de Don Cross. Je remercie ce dernier pour avoir autorisé cette adaptation.
| >II.A. L'unité FOURIER.PAS |
L'unité FOURIER.PAS, contenue dans TPMATH1.ZIP fournit les procédures de calcul de la transformée de Fourier.
| >II.A.1. Nombre maximal de points |
Le nombre de points soumis à la transformée de Fourier rapide doit être une puissance entière de 2. La valeur maximale de l'exposant (donc du nombre de points) est fonction de la taille maximale des tableaux de réels, elle-même définie dans MATRICES.PAS par la valeur de la constante MAX_FLT. L'exposant maximal (MaxPower) est calculé par la formule :
MaxPower := Trunc(Log2(MAX_FLT)); | l |
où Log2 est la fonction logarithme de base 2 (définie dans FMATH.PAS).
MAX_FLT, et donc MaxPower, dépend du type de réel choisi. Avec les réglages par défaut les valeurs possibles sont :
| l | Les valeurs de MAX_FLT sont données pour un compilateur 16 bits (TP/BP). Elles peuvent être augmentées si l'on utilise un compilateur 32 bits tel que FPK ou GNU Pascal. Cela permettrait de traiter un plus grand nombre de points. |
| >II.A.2. Procédures et fonctions |
Les procédures et fonctions suivantes sont disponibles dans FOURIER.PAS :
procedure FFT(NumSamples : Integer;
RealIn, ImagIn, RealOut, ImagOut : PVector);
| l |
Cette procédure calcule la transformée de Fourier. La signification des paramètres est la suivante :
En entrée ------------------------------------------------------------ NumSamples = Nombre de points (doit être une puissance de 2) RealIn = Signal d'entrée (Partie réelle) ImagIn = Signal d'entrée (Partie imaginaire) En sortie ------------------------------------------------------------ RealOut = Transformée de Fourier (Partie réelle) ImagOut = Transformée de Fourier (Partie imaginaire) | l |
| l | Pour la signification du type PVector, voir le cours sur le calcul matriciel. |
procedure IFFT(NumSamples : Integer;
RealIn, ImagIn, RealOut, ImagOut : PVector);
| l |
Cette procéure calcule la transformé inverse, c'est-àdire qu'elle reconstitue un signal à partir de sa transformée de Fourier.
La signification des paramètres est la même, sauf qu'ici (RealIn, ImagIn) contiennent la transformée de Fourier, alors que (RealOut, ImagOut) contiennent le signal reconstitué.
procedure FFT_Integer(NumSamples : Integer;
RealIn, ImagIn : PIntVector;
RealOut, ImagOut : PVector);
| l |
Cette procédure calcule la transformée de Fourier dans le cas où les entrées sont de type entier.
La procédure FFT_Integer_Cleanup doit être appelée après chaque appel de FFT_Integer.
procedure FFT_Integer_Cleanup; | l |
Cette procédure libère la mémoire allouée par FFT_Integer.
procedure CalcFrequency(NumSamples, FrequencyIndex : Integer;
RealIn, ImagIn : PVector;
var RealOut, ImagOut : Float);
| l |
Cette procédure calcule la transformée de Fourier en un point d'indice FrequencyIndex (compris entre 0 et NumSamples - 1) au moyen de la formule (2). Quoique plus lente que la FFT, elle peut être utile si l'on ne s'intéresse qu'à quelques points particuliers, ou si le nombre de points n'est pas une puissance de 2.
| l | Cette procédure utilise la technique d'optimisation des calculs trigonométriques décrite par Don Cross. |
| >II.B. Programme de démonstration |
Le programme TESTFFT.PAS, disponible dans TPMATH2.ZIP, montre comment utiliser la transformée de Fourier pour filtrer un signal. Le programme trace divers graphiques et écrit ses résultats dans le fichier de sortie FFTOUT.TXT.
L'exemple est un signal sinusoidal à 200 Hz contaminé par un signal parasite à 2000 Hz. La fréquence d'échantillonnage (SamplingRate) est 22050 Hz, le nombre de points (NumSamples) est 512 (= 29). Le graphe du signal d'entrée est le suivant:

Le programme calcule la transformée de Fourier et affiche le résultat sous la forme suivante (La courbe rouge correspond à la partie réelle, la courbe verte à la partie imaginaire.) :

Le milieu de la courbe représente la fréquence de Nyquist, soit 11025 Hz. La partie gauche de la courbe correspond aux fréquences positives, la partie droite aux fréquences négatives.
L'examen du fichier de sortie FFTOUT.TXT montre que le grand pic est situé à l'indice 5 et le petit pic à l'indice 46. Les fréquences correspondantes sont :
22050 x 5 / 512 ~ 215 Hz | l |
Le grand pic correspond donc au signal principal et le petit pic au signal parasite. Pour filtrer ce dernier, le programme met à zéro toutes les valeurs de la transformée de Fourier correspondant aux fréquences supérieures à 1000 Hz en valeurs absolues, d'où le code suivant :
FreqIndex := Trunc(1000.0 * NumSamples / SamplingRate);
for I := 0 to NumSamples - 1 do
begin
if ((I > FreqIndex) and (I < NumSamples div 2)) or
((I >= NumSamples div 2) and (I < NumSamples - FreqIndex)) then
begin
RealOut^[I] := 0.0;
ImagOut^[I] := 0.0;
end;
end;
| l |
L'appel de la procédure IFFT permet alors de reconstituer le signal filtré, lequel s'affiche sous la forme suivante :

On retrouve donc le signal principal, au prix d'une légère distorsion aux extrêmités.
Le programme teste ensuite, sur un signal aléatoire, le calcul direct de la transformée de Fourier par la procédure CalcFrequency. Les r&ésultats sont stockés dans le fichier FFTOUT.TXT en même temps que ceux de la FFT.